前の記事ではファジィ理論の概要と基本である傾斜型を説明しました。
本記事では三角形型について説明します。

• 第1回：ファジィ理論の概要と傾斜型
• 第2回：三角形型(本記事)
• 第3回：台形型

三角形型

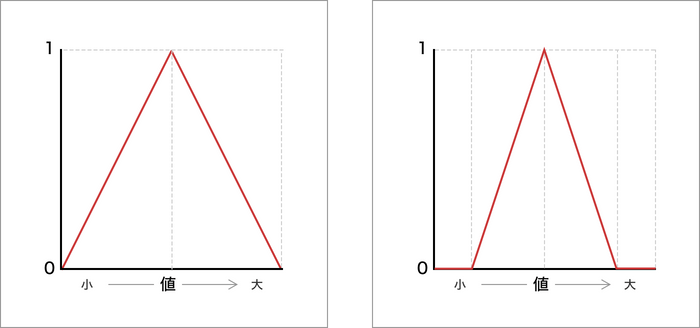
ファジィ理論の三角形型は傾斜型と逆傾斜型を組み合わせたものになります。

図のように頂点が1で頂点を超えると反転して0へと向かいます。
例えば、スクロールしてブラウザの中心に一番近い要素を選択するといった時に使えます。

利用するパラメータは4つです。

• value … キーとなる数値
• min1 … 0〜1へ向かう右肩上がりの始端
• max … 頂点
• min2 … 1〜0へ向かう右肩下がりの終端

// 三角形型
function Triangle(value, min1, max, min2) {
  // 始端、終端の範囲外なら常にゼロ
  if (value <= min1 || value >= min2) return 0

  // 頂点
  if (value === max) return 1

  // maxより小さい場合は右肩上がり
  if (value < max) return Grade(value, min1, max)

  // 1〜0へ向かう
  return ReverseGrade(value, max, min2)
}

// 傾斜型
function Grade(value, min, max) {
  if (value <= min) return 0
  if (value >= max) return 1

  const diff = max - min
  return (value / diff) - (min / diff)
}

// 逆傾斜型
function ReverseGrade(value, min, max) {
  if (value <= min) return 1
  if (value >= max) return 0

  const diff = max - min
  return (max / diff) - (value / diff)
}

See the Pen Fuzzy – Triangle by Nobuyuki Kondo (@artprojectteam) on CodePen.0

サンプル

集中力のピークを設定し、現在時刻における集中力をパーセントで表示したりすることもできます。

See the Pen Fuzzy – Triangle – Sample by Nobuyuki Kondo (@artprojectteam) on CodePen.0

ファジィ理論の関連記事

• 第1回：ファジィ理論の概要と傾斜型
• 第2回：三角形型(本記事)
• 第3回：台形型

※関数化したtipsをGitHubにアップしています